Multi-agent reinforcement learning (MARL) is pretty tricky. Beyond all the challenges of single-agent RL, interactions between learning agents introduce stochasticity and nonstationarity that can make tasks harder for each agent to master. At a high level, many interesting questions in MARL can be framed in ways that focus on the properties of the interactions between abstract agents and are ostensibly agnostic to the underlying RL algorithms, e.g. “In what circumstances do agents learn to communicate?”. For such questions, the structure of the environment/reward function/etc is usually more important.

While state of the art deep RL algorithms may not be critical for multi-agent experiments, achieving the degree of stability and robustness necessary to empirically study such questions can be challenging.

The most time consuming part of creating a scaffolding for running MARL experiments has been implementing and tuning RL algorithms that can perform well in the stochastic and partially observable gridworld environments I care about.

I spent a few weeks(!) struggling to find hyperparameters and algorithmic improvements that would allow my DRQN implementation to perform well in a variety of Marlgrid environments. I got slight improvements by messing with the model architecture and optimizer, simplifying the environment, shaping the action space and implementing PER. Still I’d begun to worry that the middling performance was due not to fixable shortcomings of the algorithm, but to crippling bugs with Marlgrid or serious issues with my intuition about the difficulty of the tasks I’d been trying to solve. This was frustrating because the RL performance I was fighting for is only of incidental importance to the questions I’d like to study.

Then I implemented PPO (Schulman et al. 2017). It immediately blew DRQN out of the water – with essentially no time spent on fussy tuning or optimization. I immediately saw huge increases in stability, robustness, and efficiency.

Tasks that DRQN could solve in hours, PPO could solve in minutes. With DRQN I struggled to find hyperparameters that would work for both small and large cluttered gridworlds; the first set of hyperparameters I used for PPO worked for all all the gridworld tasks I’d been looking at – as well as Atari Breakout!

This was extra satisfying because I didn’t use the tricks that are typically employed to ease learning for RL agents playing Atari games (frame skipping/stacking, action repeating, greyscale conversion, image downsizing). As a bonus: my PPO implementation reused the bits of my DRQN code of which I was most suspicious; good performance with PPO confirmed that these weren’t broken.

PPO

I implemented PPO (code here) using the PyTorch Spinning Up code as a reference. I highly recommend studying the Spinning Up docs for more details about PPO and other modern deep RL algorithms.

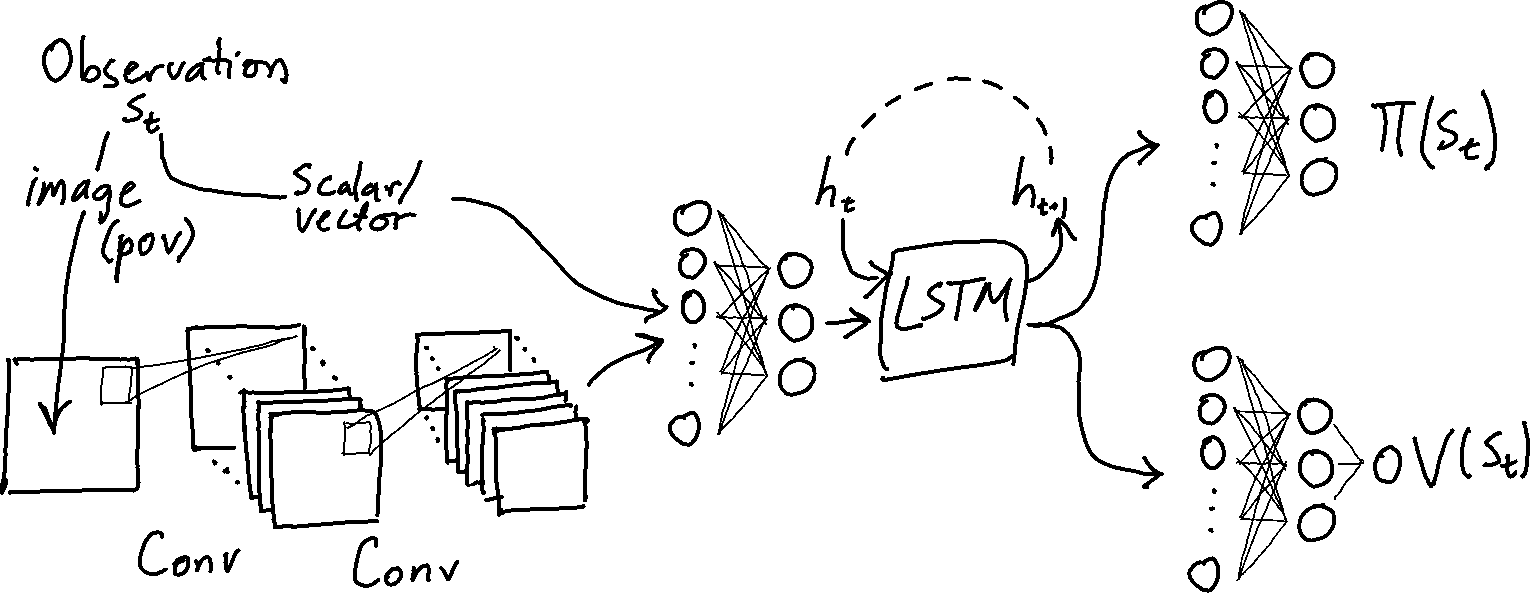
There are some substantive differences between my implementation and the spinning up reference. I include an LSTM to make sure the network can learn effective strategies in partially observable environments. As in my DRQN implementation, agents save hidden states while collecting experience. These saved hidden states are used during parameter updates.

In Spinning Up, the policy and value networks have separate weights and are separately updated with batch gradient descent (with Adam) – policy first, then value. In my implementation, the policy and value networks share most of their parameters; the heads that compute the policy $\pi(s_t)$ and value $V(s_t)$ of a state $s_t$ branch off after the LSTM. The parameters in the unified network are updated together (with minibatch Adam) to minimize the combined policy loss and value loss $(L_v + L_\pi)$.

Why didn’t I use PPO to begin with?

On-policy algorithms like PPO only update the policy parameters using data collected w/ the most recent version of the policy, while off-policy algorithms like DRQN can learn from older data. This makes off-policy RL potentially more effective in circumstances where collecting environment interactions is costly. Since I have access to <1% of the compute used to collect experience for those spectacular PPO results, I figured DRQN might be a better choice. In retrospect there are a few issues with this reasoning. First: while I (still) find the argument for off-policy sample efficiency to be somewhat compelling, I probably shouldn’t have used it as evidence that DRQN specifically is more sample efficient than PPO specifically. PPO is one of the best on-policy RL algorithms; it would be fairer to compare its sample efficiency with a state of the art off-policy RL algorithm like TD3 or SAC.

More importantly: to the degree that I care about efficiency, I care about overall (wall/cpu time) efficiency rather than sample efficiency in particular. Sample efficiency is more important in domains where interacting with the environment is slow or costly (robotics, or leaning from humans). But collecting experience in Marlgrid is fast (on my desktop, I can collect about a billion frames of experience in a day), so sample efficiency is not much of a concern.

From a bird’s eye view, I could have taken the impressive results with Dota 2/Rubik’s cube manipulation as evidence that PPO is a good choice. But these systems made use of far more computation resources than I have access to: OpenAI used 64 GPUs and 920 CPUs while collecting experience to train agents to manipulate Rubik’s cubes, and 512 GPUs and 51200 CPUs to train its team of Dota agents. I was hesitant to conclude that PPO would also be effective at my much smaller scale (1 CPU, 1-2 GPUs). But as it turns out, PPO has excellent downward scalability.

Tuning DRQN vs PPO

I found that PPO easily outperformed DRQN in the tasks I’ve been studying. Another key advantage of PPO is that it was much less finicky. Performance with DRQN was inconsistent and unstable, and I spent lots of time adjusting parameters and adding features to mitigate these issues.

If a PPO agent is struggling to make headway on a task, there are a few go-to parameters that seem to dramatically increase its chance of success: learning rate and batch size. There’s clear tradeoff between training speed (faster when learning rates are higher and batch sizes are lower) and the complexity of tasks that an agent can solve.

With DRQN it was tough to find hyperparameters that would allow stable training. And even for tasks that DRQN could “solve”, performance would sometimes drop after long periods of good behavior. I added a few tweaks that help with performance and stability:

• Target Q network
  • Very standard trick for avoiding value function overestimation
• Entropy-regularized Q function and Boltzmann exploration
  • These are standard features for contemporary DQN (i.e. default in tf-agents DQN)
• Hidden state refreshing (R2D2-style)
• Prioritized experience replay The best Q learning based RL algorithms (like the Rainbow algorithm from Hessel et al. at Deepmind) involve even more tweaks such as N-step learning, dueling DQN, and distributional RL.

The parameter controlling entropy regularization was particularly important; there seemed to be a task-specific range of acceptable values. If it was too high or too low, learning would be less stable.

I also tried (to no avail)

• changing the optimizer and learning rate
  • RMSProp seems to work much better for DRQN, but Adam is better for PPO
• changing the network architecture
  • LSTM hidden size, number/configuration of conv layers
• dramatically increasing the size of the replay buffer

References

John Schulman et al. Proximal Policy Optimization Algorithms. arXiv preprint arXiv:1707.06347, 2017.

Joshua Achiam. Spinning Up in Deep Reinforcement Learning. 2018.

OpenAI et al. Solving Rubik’s Cube with a Robot Hand. arXiv preprint arXiv:1910.07113, 2019.

OpenAI Five. Blog post, 2018.

Hessel et al. Rainbow: Combining Improvements in Deep Reinforcement Learning. arXiv preprint arXiv:1710.02298.